Osiem rozwiązań

Nieprzechodniość przyjaźni (pomimo znanego powiedzenia, że przyjaciele moich przyjaciół są moimi przyjaciółmi), poruszona kilka tygodni temu , jest wyraźnie związana z paradoksem Soritesa. Ponieważ, jakkolwiek mała, zawsze istnieje „odległość” (idei, charakteru, zachowania itp.) między dwojgiem ludzi. Zatem suma odległości może stać się odległością nie do pokonania, tak jak sklep, który znajduje się blisko sklepu, który znajduje się blisko sklepu, który znajduje się blisko sklepu… który znajduje się blisko twojego domu, może znajdować się po drugiej stronie miasta, jeśli tylko zapewnimy wystarczającą liczbę odległości.

Jeśli chodzi o osiem kwestii poruszonych w zeszłym tygodniu, niektóre odpowiedzi są krótkie lub jedynie fragmentaryczne, a inne bardziej szczegółowe:

1. Powiedziano nam, że kobieta nie ma ciemnej karnacji, a osoba o blond włosach odpowiada, że musi mieć białe włosy, ergo…

2. Jeśli chodzi o podzielenie trójkąta rozwartego na kąty ostre, łatwo dojść do błędnego wniosku, że jest to niemożliwe (Martin Gardner powiedział, że w swoich czasach otrzymał kilka „dowodów” takiej niemożliwości), ponieważ bez względu na to, jak bardzo go podzielimy, zawsze powstanie co najmniej jeden mały i oporny kąt rozwarty, taki jak ten w prawym dolnym wierzchołku figury.

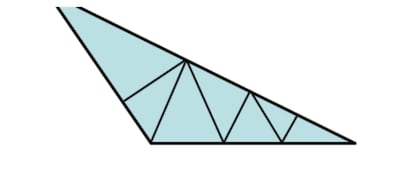
Jednak podział jest możliwy i jako wskazówkę powiem, że to jeden z tych pouczających problemów, w których nieświadomie narzucamy sobie więcej warunków, niż jesteśmy zobowiązani spełnić. Czym w tym przypadku jest ten nieświadomy, nieproszony warunek?

3. Braci Marx było pięciu: Chico, Groucho, Harpo, Gummo i Zeppo; ale na potrzeby naszej zagadki najbardziej prawdopodobnym rozwiązaniem jest to, że było ich czterech (jak w ich najsłynniejszych filmach), a trzech z nich było leworęcznych. Rozwiązanie nie jest jednoznaczne: braci mogłoby być 21, z czego 15 leworęcznych. Czy istnieje jakieś inne rozwiązanie, nawet jeśli jest ono demograficznie mało prawdopodobne?

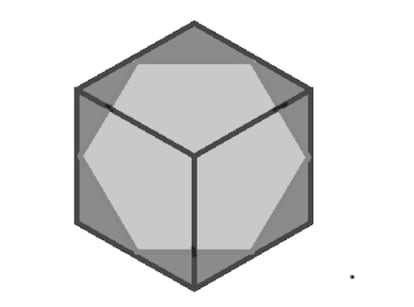
4. Jeżeli płaszczyzna przekroju przechodzi przez środki sześciu krawędzi sześcianu, otrzymamy sześciokąt foremny.

5. 129 + 438 = 567 (Czy to rozwiązanie jest unikalne?).

6. Jeśli OODDF jest pierwiastkiem kwadratowym liczby WONDERFUL, O nie może być większe od 2, ponieważ jej kwadrat miałby dziesięć cyfr, i nie może być równe 1, ponieważ kwadrat liczby zaczynającej się od 11 nie może mieć 1 w drugiej cyfrze; zatem O = 2. Szukana liczba będzie zatem znajdować się pomiędzy kwadratami 22 000 i 23 000, a ponieważ drugą cyfrą liczby WONDERFUL jest 2, W = 5… Podążając tym tokiem rozumowania, otrzymujemy WONDERFUL = 523 814 769.

7. Największy okrąg, który przechodzi tylko przez białe kwadraty, ma środek w środku białego kwadratu i przechodzi przez najdalsze wierzchołki czterech czarnych kwadratów, które go otaczają. (Jaki jest jego promień?)

8. Pociągi zbliżają się z prędkością względną 130 + 170 = 300 km/h, więc na 5 minut przed zderzeniem będą oddalone od siebie o 25 km. Początkowa odległość nie ma znaczenia; służy jedynie do zmylenia.

Gry nieprzechodnie

Odnosząc się do nieprzechodniości, Salva Fuster skomentował: „Nieprzechodnie kostki do gry to jeden z najbardziej zaskakujących przypadków, jakie znam. Myślę, że większość osób, które po raz pierwszy widzą nieprzechodnie kostki do gry, próbuje znaleźć błąd, licząc przypadki, w których każda kostka pokonuje inną”. Bardzo prawdziwe i interesujące, na tyle, że warto poświęcić temu tematowi kolejny wpis. A żeby zaostrzyć ciekawość, pomyśl o innej grze nieprzechodniej. Są co najmniej dwie bardzo popularne…