Colombe feroci

La settimana scorsa ci siamo chiesti quanti triangoli equilateri più piccoli siano necessari, come minimo, per coprire un triangolo equilatero. Questi triangoli più piccoli non devono essere uguali e possono sovrapporsi. La risposta è 3, e ci arriviamo escludendo la possibilità più piccola: è ovviamente possibile con 3, e non è difficile dimostrare (come?) che non è possibile con 2.

Per quanto riguarda il problema dei 5 vertici di un triangolo equilatero sono stati proposti diversi approcci; il più "incasellato" è quello di Francisco Montesinos:

"Unendo i punti medi dei lati del triangolo equilatero originale, otteniamo 4 triangoli equilateri con lati di 1/2 m. Due dei 5 punti dati saranno necessariamente all'interno dello stesso triangolo di quelli ridotti, quindi la loro distanza d non può essere d>1/2."

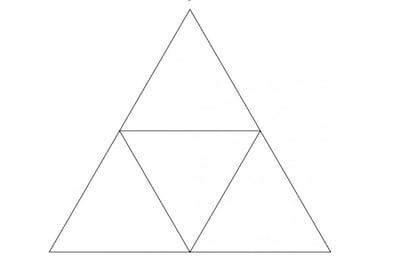
Infatti, dividendo il triangolo iniziale in 4 triangoli uguali, si crea una colombaia con 4 spazi, ognuno dei quali deve ospitare 5 piccioni, o punti. E la massima distanza che può esistere in un triangolo equilatero con lato di 1/2 m è esattamente la lunghezza del lato, quindi due punti qualsiasi situati al suo interno possono, al massimo, distare 1/2 m l'uno dall'altro (e sono, ovviamente, i vertici del triangolo).

La soluzione fornita da Rafael Granero è un po' più complicata , ma non meno interessante:

Certamente, ci sono quattro punti che devono essere i più lontani, e si potrebbe anche dire che, dati quattro punti, essi siano i più lontani possibili l'uno dall'altro: i tre vertici e il centro. Il centro dista 57,7 cm da uno qualsiasi dei tre vertici. Qualsiasi spostamento, per quanto piccolo, del punto situato al centro diminuirà inevitabilmente la distanza di uno o due dei vertici. E lo stesso vale per ciascuno dei punti situati ai vertici rispetto agli altri tre punti. Gli unici punti che distano più di 50 cm dal centro sono quelli esterni a una circonferenza di raggio 50, centrata nel centro del triangolo equilatero. Ma in ciascuna delle tre zone, tutti i punti distano meno di 8 cm dal punto più lontano, che è il vertice, quindi non c'è modo di individuare un quinto punto che dista più di 50 cm dagli altri quattro.

Come di sfuggita, è stata posta la domanda su quanto sia improbabile dover lanciare un dado 13 volte per ottenere 3 numeri uguali, e questa è la risposta di Juan Zubieta:

"La probabilità di ottenere il 13 è il quoziente delle possibili permutazioni con 6 coppie di numeri (12!/2^6) e tutte le possibili sequenze di lanci (6^12). Il risultato è: 1925/559872 (circa una probabilità su 291)." (Ricorda, non si tratta di ottenere un numero specifico, come 6, 3 volte, ma piuttosto di ottenere un numero che esca almeno 3 volte.)

Colombaia ad alto rischio

Dopo la formazione delle ultime settimane, e dedicata in particolar modo a chi pensa che il principio della casella di controllo sia un luogo comune applicabile solo ai problemi più semplici , ecco un classico che ha meritato l'attenzione dello stesso Paul Erdös:

Dato l'insieme {1, 2, …, 2n}, dimostrare che in ogni sottoinsieme di n+1 numeri ce ne saranno almeno due tali che uno sia multiplo dell'altro.

Non cercare di risolverlo nelle ore più calde: i piccioni in questa soffitta ad alto rischio potrebbero friggere le tue cellule cerebrali.